When Madonna Yoder ’17 was eight years old, she learned how to fold a square piece of paper over and over and over again. After about 16 folds, she held a bird in her hands.
The first time she pulled the tail of a flapping crane, she says, she realized: Oh, I folded this, and now it’s a toy.
That first piece was an origami classic, folded by kids at summer camp for generations and many people’s first foray into the art form. Often, it’s also the last. But Yoder was transfixed. Soon she was folding everything she could find: paper squares from chain craft shops, scraps from around the house, the weekly church bulletin, which she would cut into pieces with the aid of her fingernails. She would then “turn those into little critters and give them to any guests that were there that week,” she says.
Today, perhaps millions of folds later, Yoder is a superstar known to some as the “Queen of Tessellations,” a reference to a mathematically intricate type of origami that she began exploring during her years at MIT.
“These are patterns that can repeat infinitely and are folded on a single sheet of paper,” Yoder explains. “There’s literally no end to the patterns themselves, no end to the number of designs you can create … They’re folded by hand—I don’t know of any machine that could fold them—and they are a really great way to just sit and focus and relax.”
Her pieces have grown increasingly complex over time, but the patterns she creates are based on recognizable shapes, including hexagons, triangles, rhombuses, and trapezoids. Yoder folds and rotates them into repeating, potentially infinite series of shapes. Picture the graphic pattern in an M.C. Escher print, but made out of a single sheet of paper—a piece of art underpinned by mathematics and a bit of engineering, combined with the complexity of a snowflake.
Yoder grew up in southwestern Virginia, in the Blue Ridge Mountain town of Shawsville, where professors from Virginia Tech filled the pews at her Mennonite church. “All of us kids were expected to go to college,” she says. After she made her way to MIT, her brother, Jake, earned his PhD in materials engineering at Virginia Tech and now works with 3D-printed metals. Her mother, Janet, is a physical therapist and her father, Denton, is a computer systems engineer at Virginia Tech.
From a young age, Yoder had an inclination for making things with her hands. “I was kind of that kid—I did all the different crafts. I did a lot of cross-stitch,” she says, including a portrait of her grandmother that now hangs framed in her kitchen.
She also remembers an early appreciation for accuracy. “My mom tells the story about when I was five years old, we were cutting out squares, and I was like: ‘Mom, your squares are not precise enough,’” she says.
Toward the end of her senior year of high school, Yoder won a math competition, which came with an apt prize: a book about modular origami, in which multiple sheets of paper are folded and combined into often elaborate structures. She took a gap year in Peru, where she continued to fold, giving little modular pieces away to children she met on her travels.
Yoder had always done paper folding in solitude, with guidance only from books. When she arrived at MIT after her time in Peru, she was surprised to learn about weekly origami gatherings and the annual convention held by the campus club OrigaMIT.
“It took until I got to MIT to realize that, oh, this is an active space where people are meeting up and designing things and talking to each other about origami all weekend,” she says. She majored in Earth, Atmospheric, and Planetary Sciences (EAPS), but in the spring of her senior year, she took Erik Demaine’s popular class Geometric Folding Algorithms—and discovered that “origami research was something that people got paid to do,” as she puts it. Her final project for the class became a poster presentation at the 7th International Meeting on Origami in Science, Mathematics, and Education (7OSME). “In that course, I got hooked on origami research,” Yoder says.
Demaine remembers that Yoder started to explore concepts related to tessellations in his class, which eventually led to the publication of her first paper—“Folding Triangular and Hexagonal Mazes,” coauthored with him and Jason Ku, then a lecturer at MIT. In that paper, Yoder helped demonstrate how to “generalize” a square grid maze to triangular and hexagonal grids by changing the underlying crease pattern. “We probably suggested this as an interesting open problem for people to work on, and Madonna found a really happy niche there,” says Demaine, who isn’t aware of any other former students pursuing careers in origami. “We provided the space for her to do the research, but then she went whole hog on it.”
But she didn’t truly embrace tessellations until after she graduated and was preparing for a four-and-a-half-month MIT-sponsored internship in Israel. “These modulars have a lot of volume—I’m not going to bring back a suitcase full of them,” she remembers thinking. And she wasn’t going to leave behind four-plus months of folding work. “So I decided to teach myself to fold tessellations because they’re flat and travel well,” she says. “Then it took root in my brain and never let me go.”
But there was the practical matter of making a living.
Origami principles have been used to conceive of and develop a wide range of things, from the tiny (think medical instruments or nanoscale devices that can deliver DNA into cells) to the large (such as collapsible structures usable in disaster response or foldable solar arrays for space exploration). Yoder figured if she wanted to pursue origami as a career, she would have to do it as a scientist or engineer.
But after reverse-engineering hundreds of origami patterns she found online—and starting to design her own—she began to suspect otherwise. “I realized it’s actually possible to make a living as an origami artist,” she remembers. “I won’t say that now, five years out from that decision, I’ve reached a point of being able to fully financially support myself with origami, but thankfully, I married a software engineer.” (She met her husband, Manny Meraz-Rodriguez, while the two were working at the Lawrence Livermore National Laboratory, she as an intern and then as a postcollege appointee in computational geoscience.)
Origami purists will say that true origami requires no cuts, no glue. The only slicing Yoder does is with a rotary cutter she uses to make hexagonal pieces of paper, stacks at a time. Though she starts with squares sometimes, the hexagon is her favored launching pad. She creases the paper into a grid, and then—following a design that she’s created using a vector graphics program called Inkscape—begins to fold.
“The main reason why I draw the patterns out first, besides the fact that the designs have gotten too complicated for me to hold in my brain and solve on the fly, is because I like to have the pattern rotated so that the repeats of the pattern align with the edge, which you can only do if you have the information of how the repeats of the pattern line up with the background grid,” she explains.
Using a simple tool called a bone folder (Yoder says she’s had hers for years and could pick it out of a pile by the wear pattern), she presses and creases and rotates the paper into an elaborate pattern that could, in theory, go on forever. The end result is a beautiful, satisfyingly symmetrical array of repeated, interlocking shapes that look especially impressive when held up to the light, bringing to mind a stained-glass window.

Scholars debate whether the ancient tradition of origami began in Japan or China, but the art really took off globally in the 1950s and ’60s when publishers printed and mass-marketed diagrams showing people how to fold paper into figurative objects such as birds, fish, and animals. Paper tessellations have roots in Germany in the 1920s, when the artist Josef Albers added folding to his introductory design course at the Bauhaus. This geometric tradition started gaining popularity in the 1980s and 1990s, and now, Yoder says, there are perhaps tens of thousands of people who participate. The broader universe of origami practitioners likely numbers in the millions.
These aficionados attend conferences, watch YouTube videos, and take online courses, most of them to learn existing patterns. Yoder creates her own: In addition to the peer-reviewed academic papers she’s authored on the mathematical underpinnings of her tessellations (with titles like “Symmetry Requirements and Design Equations for Origami Tessellations” and “Hybrid Hexagon Twist Interface”) and regular presentations at origami conferences across the globe, she’s designed 696 original patterns. Each year in an event she calls Advent of Tess, she teaches thousands of online participants a new design every day of December leading up to Christmas, and her website, Gathering Folds, has become a go-to source, not just for Yoder’s artwork but for instruction.
Her EAPS degree from MIT may not seem like a foundation for a career as an artist, but Yoder, who studied geology with a secondary focus on ecology, says there are connections between the fields. “There is a lot of carryover between the crystal structures and the tessellation symmetries,” she explains. “Every repeating 2D pattern obeys one of the planar symmetry groups … There are things that repeat like a hexagon, things that repeat like a square, things that repeat like a triangle, and things that repeat like a parallelogram or rectangle. And then there are things that are not rotationally symmetric. Those ideas of how things connect and how things repeat definitely carry over from my crystallography class.”
Yoder cites the origami artist and physicist Robert Lang as one of the current practitioners who influenced her the most. He, like Yoder, has a math and science background but forged a career in art.
“The thing that has set her above the current crowd is that she’s really systematically explored the building blocks of tessellations and the different little patterns that can be considered building blocks, and the rules for connecting these blocks,” he explains. “Madonna’s knowledge and understanding of mathematics and geometry gives her a broader tool kit to create art, and that’s led to her success as an artist. You can’t separate the art from the science background. It’s part of the thinking process, even if the end goal is very much in the fine art world.”
For Yoder, the process, both computational and tactile, is also an end in itself. It is almost a meditation—a way to slow down and contemplate. Some of her students have even suggested there might be a spiritual component to it. One said to her: “You know, the name for that connection to infinite things is called God, right?”
“So I kind of leave that more open,” she says. “I’m not super decided about what these things mean. I’m just happy to have that spark when I’m designing a pattern: Here’s how the shapes hang together, and now that I’ve drawn out those shapes, I can copy and paste, paste, paste, paste, paste, and it just clicks in very satisfyingly.”
Yoder has considered whether she will ever get bored pursuing the possibilities of infinite patterns—whether she will achieve perfection and decide to put the bone folder away for good.
“But I’m not convinced that I will,” she says. “There are always ways to make it harder and harder.”
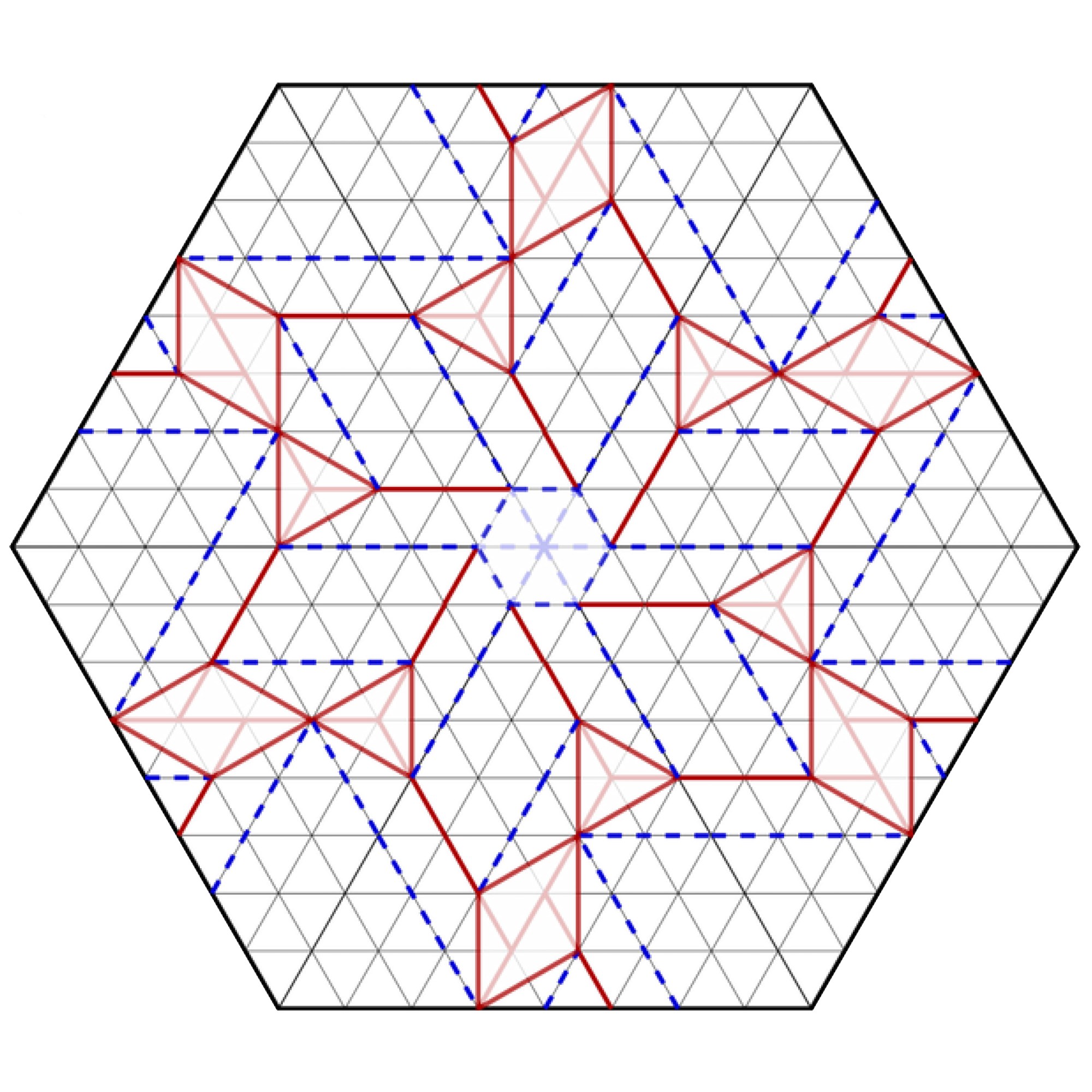

Fold it yourself
Try your hand at folding Madonna Yoder’s Dancing Ribbons tessellation design featuring three closed twists: hexagon, triangle, and rhombus.
Basic instructions
1. Download the pattern here and cut out the hexagon with the crease pattern.
2. Fold all the background grid lines, making sure to fold them back and forth so the paper is ready to form the pattern. (You can precrease all the off-grid folds too, but Yoder recommends folding one twist at a time.) This pattern shows mountain folds with solid red lines and valley folds with dashed blue lines. The faded lines inside the twists are helper folds used to set up the twists; they will not be used in the final pattern.
3. Working from the side without the pattern, fold the central hexagon.
4. Fold the triangles.
5. Fold the rhombuses.
Find more detailed instructions and a video tutorial—as well as paper advice—at technologyreview.com/tessellation.
You can also sign up for Yoder’s annual Advent of Tess—a 25-day folding challenge that begins December 1—at https://training.gatheringfolds.com/advent.